반응형
SMALL
삼각형

- 삼각형은 세 개의 정점(꼭지점 혹은 Vertex) 으로 이루어진다.
- 정점으로 세 개의 변(edge)이 정해진다.
- 삼각형의 세변중 두 개의 변이 이루는 각을 내각(interior angle) 이라고 한다.
- 세 개의 내각의 합은 항상 180도 이다.
- 삼각형은 항상 어딘가의 평면 위에 존재한다.
직각삼각형

- 삼각함수에서 다루는 삼각형 이다.
- 세개의 정점부분의 내각 중 하나가 직각(90도)을 이룬다.
- 비스듬한 변을 빗변(hypotenuse), 바닥에 있는 것을 밑변(adjacent), 남은 변을 높이(opposite) 라고 한다.
- 세변의 길이와 빗변과 밑변이 이루는 내각의 각도인 θ(세타, theta) 사이의 관계를 이용해 빗변과 세타가 주어졌을때 다른 두 변의 길이를 산출하는 것이 삼각함수의 가장 기본적인 쓰임세.
피타고라스의 정리
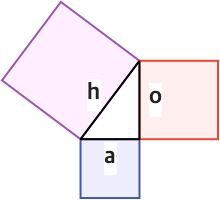
- 빗변의 길이를 h, 밑변의 길이를 a, 높이의 길이를 o로 했을때 다음 식이 성립한다.
- h² = a² + o²
- 예를 들어 a = 3, o = 4 일때 는 h² = 9 + 16 이기 때문에 h = 5라는 결론이 나온다.
사인, 코사인, 탄젠트
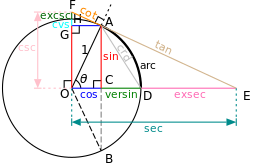
- 직각삼각형에서 변을 두개 선택할시 두 변의 길이의 비율 (삼각비)는 θ의 각도에 따라 변화한다.
- 매개변수 θ세타의 값을 안다면 각 변수 사이의 관계를 나타낼 수 있다.
- 변이 3개 이므로 총 3개의 식 사인, 코사인, 탄젠트가 있다.
- 아래는 C가 직각인 삼각형 ABC에서, 각 A, B, C의 대변(마주보는 변)의 길이를 a,b,h라고 할 때, 사인, 코사인, 탄젠트의 정의.


다음 포스팅은 삼각함수 3개의 식인 사인 코사인 탄젠트에 대해 포스팅
반응형
LIST
